It all starts with a question:

How to sample from a given distribution?

The simplest method

Let's say, how to sample from \(Uniform(0, 1)\)?

Actually the random() function, which is a pseudo-random number generator, have already solved the problem for us. It can generate a sequence of numbers whose properties approximate the properties of sequences of random numbers obeying uniform distribution.

Moreover, we can sample from normal distribution by utilizing Box-Muller transform.

Box-Muller transform

If random variables \(U_1, U_2 \overset{\text{iid}}{\sim} U(0,1)\), and

\[\begin{align} Z_1=\sqrt{-2\ln{U_1}}cos(2\pi U_2) \\ Z_2=\sqrt{-2\ln{U_1}}sin(2\pi U_2) \end{align}\]

then \(N_1, N_2 \overset{\text{iid}}{\sim} \mathcal{N}(0,1)\)

Some other common continuous distribution e.g. exponential distribution, gamma distribution, beta distribution and t-distribution could also be sampling with similar math transform. However, when sampling from more complicated distributions or high dimensional distributions, it's not so easy to find such a transform. Here, complex sampling method will be used, and the algorithms we're going to introduce, MCMC(Markov Chain Monte Carlo) and Gibbs sampling are two of them that are commonly used.

Some other methods

Before looking directly at our goals, I'd like to introduce some other sampling methods first.

Rejection sampling

Also called accept-reject method. Given a distribution with p.d.f. \(p(x)\). Suppose there is another simple distribution function \(q(x)\) from which we can sample easily. If there exist a constant \(M<\inf\) that for all \(x\in\mathbb{R}\),

\[p(x)\leq Mq(x)\]

then we can sample from \(p(x)\) with the following method:

for i = 1 to N:
    Generate u ~ U(0, 1) and x ~ q(x)
    if u < p(x) / (M * q(x)):
        x is accepted as a sample
        i += 1
    else:
        continue

It can be easily proved that this algorithm works.

Importance Sampling

Say if we want to know the expectation of \(f(x)\), i.e. \(\operatorname{E}[f(x)]\), in which the random variable \(x\) follows a distribution \(p(x)\). Also, consider another simple distribution function \(q(x)\) that can be easily sampled. Then

\[ \hat{E}=\int_x{f(x)p(x)dx}=\int_x{f(x)\frac{p(x)}{q(x)}q(x)dx}\]

Let \(w(x)=\frac{p(x)}{q(x)}\), the last formula can be seen as \(\operatorname{E}[f(x)w(x)]\) in which \(x\sim q(x)\). As we can easily sample from \(q(x)\),

\[\hat{E}=\frac{1}{N}\sum\limits_{i=1}^N{f(x^{(i)})w(x^{(i)})}\]

in which \(x^{(i)}\) is the \(i\)-th sampled \(x\) from \(q(x)\). Here \(w(x)\) is called importance weight.

Markov chain Monte Carlo

MCMC methods comprise a class of algorithms for sampling from a probability distribution. bMarkov Process, Markov Chain & Hidden Markov Model

Markov process

Markov process is a stochastic process that satisfies the Markov property, i.e. the conditional probability distribution of future states of the process depends only upon the present state.

Markov chain

Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.

For a Markov chain with finite state space, the transition probability distribution can be represented by a matrix, called the transition matrix, with the \((i, j)th\) element of \(P\) equals to \[ p_{ij}=\Pr(X_{n+1}=j\mid X_{n}=i) \] A Markov chain is called time-homogeneous if the transition matrix \(P\) is the same after each step.

If the Markov chain is irreducible and aperiodic, then there is a unique stationary distribution π. \[ \pi\mathbf{P}=\pi \] There are three several important properties for those fully connected (namely for all \((i,j)\) in \(P\), \(\exists n\in\mathbb{N^+} \text{ such that }P^n_{ij}\neq0\)), aperiodic, time-homogeneous Markov chain.

\[ \begin{equation} \lim_{n\rightarrow \infty}{P^n}= \begin{bmatrix} \pi\\\pi\\\vdots\\\pi\\ \end{bmatrix} = \begin{bmatrix} \pi(1)&\pi(2)&\cdots&\pi(j)&\cdots\\ \pi(1)&\pi(2)&\cdots&\pi(j)&\cdots\\ \vdots&\vdots&\ddots&\pi(j)&\cdots\\ \pi(1)&\pi(2)&\cdots&\pi(j)&\cdots\\ \vdots&\vdots&\vdots&\vdots&\vdots\\ \end{bmatrix} \end{equation} \]
\[ \pi(j)=\sum_{i=0}^{\infty}\pi(i)P_{ij} \]
\(\pi\) is the only non-negative solution of equation \(\pi\mathbf{P}=\pi\)

Detailed balance condition

A Markov chain is said to be reversible if there is a probability distribution \(\pi\) over its states such that \[ \pi _{i}\Pr(X_{n+1}=j\mid X_{n}=i)=\pi _{j}\Pr(X_{n+1}=i\mid X_{n}=j) \] the detailed balance equation can be written as \[ \pi _{i}p_{ij}=\pi _{j}p_{ji}\, \]

which indicates that, for each pair of states \((i, j)\), the probability mass gained from each other should be equal to the probability mass they loss at the same time, when the stationary distribution \(\pi\) is reached.

Hidden Markov Model

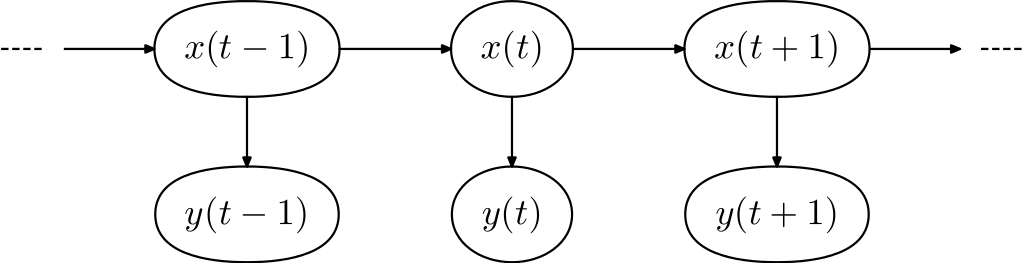
HMM is a statistical Markov model in which the system being modeled is assumed to be a Markov process with hidden states and visible output state for each hidden state. The following image describes a Markov chain. \(x(t-1)\), \(x(t)\) and \(x(t+1)\) denote the hidden states at the 3 moment, while \(y(t-1)\), \(y(t)\) and \(y(t+1)\) denote the corresponding observer states.

Metropolis–Hastings algorithm

M-H algorithm is one of the commonly used random walk Monte Carlo methods. In fact, the name Monte Carlo is suggested to use by Metropolis. As said above, MCMC is to construct a Markov chain with stationary distribution \(\pi=p(x)\), in which \(p(x)\) is the given distribution to be sampled.

Consider that we already know the given distribution \(p(x)\) and its transition matrix \(Q\). Generally we'll have \[ p(i)q(i,j)\neq p(j)q(j,i) \] We can introduce another coefficient \(\alpha(i,j)\) that will hopefully solve the problem for us, namely \[ \begin{equation} p(i)q(i,j)\alpha(i,j)=p(j)q(j,i)\alpha(j,i) \tag{*} \end{equation} \] Clearly we can let \(\alpha(i,j)=p(j)q(j,i)\) to make the equation true. If we let \(q'(i,j)=q(i,j)\alpha(i,j)\), the original equation would become: \[ p(i)q'(i,j)=p(j)q'(j,i) \] Now we have successfully constructed a Markov chain with transition matrix \(q'\) and given stationary distribution \(p(x)\). The Metropolis–Hastings algorithm is described below. Notice that \(q(j|i) = q(i,j)\).

x_{0} = x0 # Initialization
for i = 1 to N:
    Generate x* ~ q(x*|x_{i-1})
    a = min( 1, ( p(x*) * q(x*|x_{i-1}) ) / ( p(x_{i-1}) * q(x_{i-1}|x*) ) )
    Generate u ~ U(0, 1)
    if u > a:
        x_{i} = x_{i-1} # Reject
    else:
        x_{i} = x* # Accept

When \(q(i, j)=q(j,i)\) is satisfied, the algorithm is called Metropolis algorithm, in which

    a = min( 1, p(x*) / p(x_{i-1}) )

Gibbs Sampling

Gibbs sampling is a special case of the Metropolis–Hastings algorithm. Given a multivariate distribution, it's better for us to use Gibbs sampling if it is simpler to sample from a conditional distribution than to marginalize by integrating over a joint distribution. Suppose we want to obtain \(N\) samples of \(\mathbf {X}=(x_{1},\dots ,x_{n})\) from a joint distribution \({\displaystyle p(x_{1},\dots ,x_{n})}\). Gibbs sampling can be described as follows:

X_0 = X0 # Initialization
for i = 1 to N:
    for j = 1 to n:
        sample x^i_j from the distribution:
            p(x^i_j|x^i_1,...,x^i_{j-1},x^{i-1}_{j+1},...x^{i-1}_n)

Slice Sampling

Suppose you want to sample some random variable \(X\) with distribution \(f(x)\). Slice sampling can be described as follows:

x_0 = x0 # Initialization
for i = 1 to N:
    Generate y_i from U(0, x_{i-1})
    Generate x* from U(Domain of x)
    while f(x*) < y
        generate x* from U(min(x_{i-1}, x*), max(x_{i+1}, x*))
    x_i = x*

Notes about MCMC and Sampling

7月 26, 2019
科研 / Research